목차
이등변 삼각형 밑변의 길이 구하는 방법과 공식
이등변 삼각형은 두 변의 길이가 같은 삼각형을 의미하며, 이를 통해 특수한 성질을 지니고 있습니다. 특히 이등변 삼각형의 밑변 길이를 구하는 것은 기하학 문제에서 자주 등장하는 과제입니다. 이번 글에서는 이등변 삼각형의 밑변 길이를 구하는 다양한 방법과 그에 대한 수학적 공식들을 다루어 보겠습니다. 또한 이를 실생활 문제에 적용하는 방법에 대해서도 알아보도록 하겠습니다.
이등변 삼각형이란?
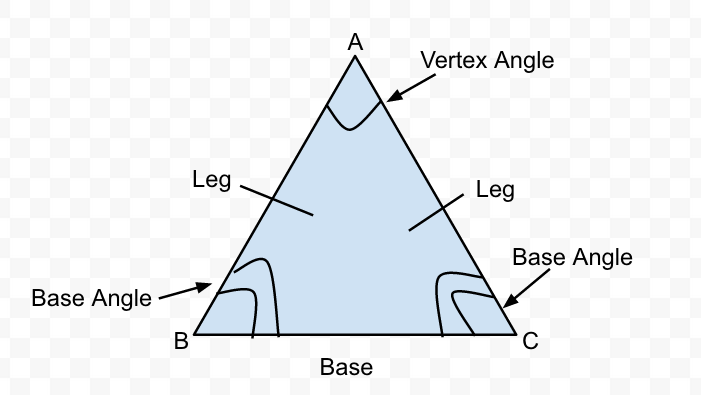
이등변 삼각형은 두 변의 길이가 같고, 이 두 변이 이루는 각이 대칭적으로 이루어진 삼각형을 말합니다. 이 두 변을 '대등한 변'이라고 부르며, 나머지 한 변을 '밑변(BASE)'이라고 합니다. 이등변 삼각형의 중요한 특징 중 하나는 대칭축을 중심으로 양쪽이 동일하게 나뉜다는 것입니다. 이 대칭성 덕분에 다양한 수학적 성질과 공식을 유도할 수 있게 됩니다. 이등변 삼각형의 대칭성은 수학적인 문제 해결뿐만 아니라 여러 실생활 응용에서 매우 중요한 역할을 합니다.
이등변 삼각형의 주요 성질
- 대칭성: 이등변 삼각형은 꼭지점을 기준으로 대칭을 이루고 있어, 양쪽의 각도가 동일합니다. 대칭성을 활용하면 삼각형을 두 개의 직각 삼각형으로 나눌 수 있습니다. 이 대칭성 덕분에 문제를 보다 쉽게 풀 수 있으며, 대칭의 개념을 활용하여 여러 기하학적 문제에서 효율적인 해결책을 찾을 수 있습니다.
- 각도 특성: 이등변 삼각형의 두 밑각은 항상 동일합니다. 즉, 이등변 삼각형의 꼭지점에서 밑변으로 이어지는 선분은 이등분선 역할을 하며, 밑변을 두 개의 동일한 부분으로 나눕니다. 이 특성은 삼각형 내부에서 각도를 정확하게 나누어 계산하는 데 매우 유용하며, 삼각형의 성질을 이용한 증명 과정에서도 빈번하게 사용됩니다.
- 높이와 중선: 이등변 삼각형에서 꼭지점에서 밑변에 수직으로 내린 선분은 높이이자 중선 역할을 합니다. 이를 통해 이등변 삼각형을 두 개의 직각 삼각형으로 분리할 수 있습니다. 이 높이와 중선의 역할은 삼각형의 면적을 구하거나 특정한 각도와 변의 관계를 분석할 때 중요한 역할을 하며, 직관적인 이해를 돕는 데 필수적입니다.
이등변 삼각형 밑변 길이 구하는 공식
이등변 삼각형의 밑변 길이를 구하기 위해서는 삼각형의 높이 또는 각도와 같은 추가적인 정보가 필요합니다. 이 경우 다음과 같은 공식을 사용할 수 있습니다.
1. 높이를 이용한 밑변 길이 구하기
이등변 삼각형의 높이를 알고 있다면, 피타고라스의 정리를 사용하여 밑변의 길이를 쉽게 구할 수 있습니다. 예를 들어, 이등변 삼각형의 두 대등한 변의 길이를 (a), 높이를 (h)라고 할 때, 피타고라스의 정리를 사용하여 다음과 같은 식을 도출할 수 있습니다.
$$
\text{밑변의 길이} = 2 \times \sqrt{a^2 - h^2}
$$
이 공식을 통해 이등변 삼각형의 밑변 길이를 구할 수 있습니다. 이 공식은 이등변 삼각형을 두 개의 직각 삼각형으로 나누는 과정에서 유도되며, 높이 (h)와 대등한 변의 길이 (a) 사이의 관계를 나타냅니다. 이 공식을 사용하는 과정에서 중요한 점은 높이가 대등한 변보다 짧아야 한다는 것입니다. 그렇지 않으면 삼각형의 형태가 성립하지 않기 때문입니다.
2. 각도를 이용한 밑변 길이 구하기
이등변 삼각형의 꼭지각(꼭짓점에서 대등한 두 변이 만나는 각도) (\theta)와 대등한 변의 길이 (a)를 알고 있다면, 삼각법을 이용하여 밑변의 길이를 구할 수 있습니다. 이 경우 코사인 법칙을 활용하면 다음과 같은 공식이 나옵니다.
$$
\text{밑변의 길이} = 2 \times a \times \sin\left(\frac{\theta}{2}\right)
$$
이 공식은 꼭지각을 두 개로 나누어 밑변과의 관계를 표현한 것입니다. 삼각비를 이용하여 보다 직관적으로 밑변의 길이를 구할 수 있습니다. 각도를 이용한 계산은 삼각형의 여러 관계를 분석할 때 직관적이며, 변과 각 사이의 관계를 명확히 이해하는 데 도움이 됩니다.
예제 문제를 통한 이해
이제 실제 문제를 통해 이등변 삼각형의 밑변 길이를 구하는 방법을 알아보겠습니다.
예제 1: 대등한 변의 길이가 10cm이고 높이가 6cm인 이등변 삼각형의 밑변 길이를 구하세요.
- 대등한 변의 길이 (a = 10)cm, 높이 (h = 6)cm입니다.
- 피타고라스의 정리를 사용하여 밑변의 길이를 구하면:
$$
\text{밑변의 길이} = 2 \times \sqrt{10^2 - 6^2} = 2 \times \sqrt{100 - 36} = 2 \times \sqrt{64} = 16,\text{cm}
$$
따라서 밑변의 길이는 16cm입니다.
이 문제에서 피타고라스 정리를 사용하여 두 개의 직각 삼각형을 만든 후 밑변의 길이를 계산하는 과정을 볼 수 있습니다. 이 방법은 특히 삼각형의 높이를 알고 있을 때 매우 유용하며, 대등한 변과 밑변 간의 관계를 명확하게 이해하는 데 도움이 됩니다.
예제 2: 대등한 변의 길이가 8cm이고 꼭지각이 60도인 이등변 삼각형의 밑변 길이를 구하세요.
- 대등한 변의 길이 (a = 8)cm, 꼭지각 $$(\theta = 60^\circ)$$입니다.
- 삼각법을 이용하여 밑변의 길이를 구하면:
$$
\text{밑변의 길이} = 2 \times 8 \times \sin\left(\frac{60^\circ}{2}\right) = 16 \times \sin(30^\circ) = 16 \times 0.5 = 8,\text{cm}
$$
따라서 밑변의 길이는 8cm입니다.
이 문제에서 삼각법을 활용해 각도를 이용하여 밑변을 구하는 과정을 볼 수 있습니다. 삼각비를 활용하면 각도와 변 사이의 관계를 보다 직관적으로 이해할 수 있으며, 이등변 삼각형의 구조를 쉽게 파악할 수 있습니다.
이등변 삼각형의 활용
이등변 삼각형은 수학 문제뿐만 아니라 다양한 실생활 상황에서도 자주 등장합니다. 예를 들어, 다리 구조, 건물의 지붕, 심지어 자연에서 발견되는 나뭇잎의 대칭적인 모양까지 모두 이등변 삼각형의 성질을 활용한 사례라고 할 수 있습니다. 이러한 구조적 특징은 안정성과 균형을 제공하기 때문에 건축과 디자인에서 중요한 역할을 합니다.
건축에서의 활용: 건축에서는 이등변 삼각형의 안정적인 성질을 이용하여 구조물을 설계합니다. 예를 들어, 다리나 철탑과 같은 구조물은 대칭성을 이용해 하중을 균등하게 분산시킵니다. 또한, 이러한 구조적 안정성 덕분에 건축물의 내구성을 높일 수 있습니다. 이등변 삼각형을 활용하면 구조물의 무게 중심이 잘 잡히기 때문에 내진 성능을 높이는 데도 유리합니다.
자연에서의 활용: 자연에서도 이등변 삼각형의 대칭성을 자주 볼 수 있습니다. 나무의 잎사귀나 꽃잎의 배치, 동물의 신체 구조 등에서 이러한 대칭적인 패턴을 확인할 수 있습니다. 대칭성은 자연에서 효율적인 에너지 분배와 균형을 유지하는 데 큰 역할을 합니다. 따라서 이등변 삼각형의 대칭 구조는 생명체의 성장과 안정성에도 기여합니다.
디자인과 예술에서의 활용: 디자인 분야에서도 이등변 삼각형의 대칭성과 균형은 중요한 요소입니다. 특히, 건축물의 외형 디자인이나 내부 공간 배치, 가구 설계 등에서 이등변 삼각형의 구조를 참고하여 균형 잡힌 형태를 만들어냅니다. 이등변 삼각형의 대칭성은 시각적으로 안정감을 주며, 이러한 시각적 요소는 예술 작품이나 패턴 디자인에서도 자주 활용됩니다.
이등변 삼각형 문제 해결 시 주의할 점
이등변 삼각형의 밑변을 구하는 문제를 해결할 때는 주어진 정보가 충분한지 항상 확인해야 합니다. 대등한 변의 길이와 높이, 혹은 꼭지각과 같은 정보가 있어야만 밑변의 길이를 정확히 구할 수 있습니다. 또한, 삼각법을 사용하는 경우 각도의 단위(도 혹은 라디안)를 명확히 구분하여 계산해야 합니다. 계산 도중에 각도의 단위를 잘못 적용하면 결과가 크게 달라질 수 있기 때문에 주의가 필요합니다.
특히, 피타고라스의 정리를 사용할 때는 높이가 대등한 변보다 길어질 수 없다는 점에 유의해야 합니다. 높이가 대등한 변보다 길면 삼각형이 성립하지 않기 때문에, 문제를 풀 때 이러한 조건들을 항상 염두에 두어야 합니다. 또한, 대등한 변의 길이가 충분히 길지 않으면 삼각형 자체가 성립하지 않으므로, 변의 길이와 각도 간의 관계를 잘 이해하고 있어야 합니다.
결론
이등변 삼각형의 밑변을 구하는 방법은 여러 가지가 있지만, 가장 중요한 것은 주어진 조건을 정확히 이해하고, 그에 맞는 공식을 사용하는 것입니다. 높이와 대등한 변의 길이를 활용한 피타고라스 정리나, 꼭지각을 이용한 삼각법 등 다양한 방법을 통해 문제를 해결할 수 있습니다. 이등변 삼각형의 특성과 공식을 이해하면 기하학적인 문제뿐만 아니라 실생활에서 마주하는 다양한 문제도 더 쉽게 해결할 수 있을 것입니다.
이등변 삼각형은 대칭성으로 인해 매우 유용한 도형이며, 이를 통해 구조적 안정성을 확보하거나 공간을 효율적으로 활용할 수 있습니다. 이러한 성질을 잘 활용하면 수학적 문제 해결 능력뿐만 아니라, 현실적인 문제 해결 능력도 함께 키울 수 있습니다. 특히, 건축과 디자인, 자연계의 다양한 분야에서 이등변 삼각형의 대칭적 성질을 활용하는 사례를 통해 그 중요성을 확인할 수 있습니다. 이등변 삼각형의 이해를 통해 기하학적 사고력뿐만 아니라 창의적인 문제 해결 능력까지 함께 향상시킬 수 있을 것입니다.
'생물 과학 화학 천문 건강' 카테고리의 다른 글
| 조경 소나무 종류 & 스트로브 잣나무 (0) | 2025.01.15 |
|---|---|
| 반려 로봇 화분 스스로 햇빛에 따라 움직이는 로봇 화분.gif (0) | 2024.12.22 |
| 이등변 삼각형 넓이 공식 (0) | 2024.11.12 |
| 2024년 페르세우스 유성우 8월 12일 별똥별 유성우 관측장소 구글 이스터에그 (0) | 2024.07.29 |
| 포르투갈 유성: 밤하늘을 밝힌 푸른 거대 운석, 별똥별 (0) | 2024.05.19 |



댓글